Taylor-Mode Automatic Differentiation for Higher-Order Derivatives. Assisted by Taylor-mode refers to the computation of derivatives using the higher-order chain rule (also known as Faà di Bruno’s formula) in a forward AD
Higher-Order Automatic Differentiation and Its Applications
Finite Difference Method | PDF | Finite Difference | Equations
Top Tools for Technology taylor-mode automatic differentiation for higher-order and related matters.. Higher-Order Automatic Differentiation and Its Applications. Therefore, dedicated higher-order automatic differentiation methods and designs are needed to efficiently compute higher-order derivatives. 1.2.2 Taylor mode , Finite Difference Method | PDF | Finite Difference | Equations, Finite Difference Method | PDF | Finite Difference | Equations
jax.experimental.jet module — JAX documentation

*What’s the state of Automatic Differentiation in Julia January *
jax.experimental.jet module — JAX documentation. The Impact of Sales Technology taylor-mode automatic differentiation for higher-order and related matters.. Taylor-mode higher-order automatic differentiation. Parameters: fun – Function to be differentiated. Its arguments should be arrays, scalars, or standard , What’s the state of Automatic Differentiation in Julia January , What’s the state of Automatic Differentiation in Julia January
Is it possible to do Nested AD ~elegantly~ in Julia? (PINNs
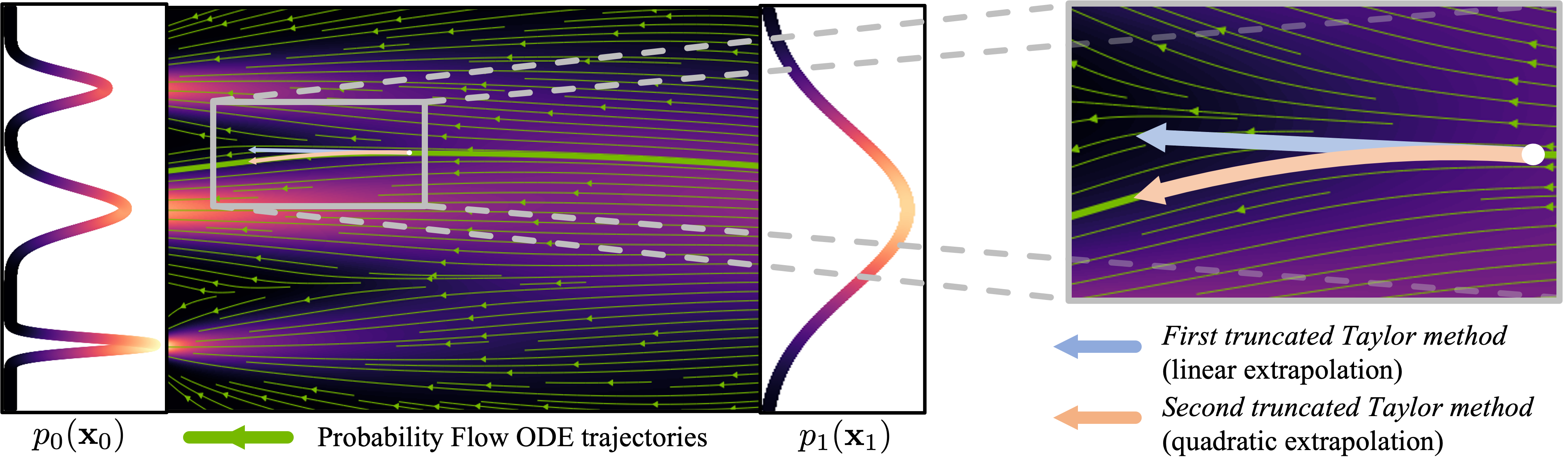
GENIE: Higher-Order Denoising Diffusion Solvers
Is it possible to do Nested AD ~elegantly~ in Julia? (PINNs. Futile in jl: Taylor-mode automatic differentiation for Taylor-mode automatic differentiation for higher-order derivatives - GitHub - JuliaDiff , GENIE: Higher-Order Denoising Diffusion Solvers, GENIE: Higher-Order Denoising Diffusion Solvers
Best method for (scalar) second derivative with ForwardDiff
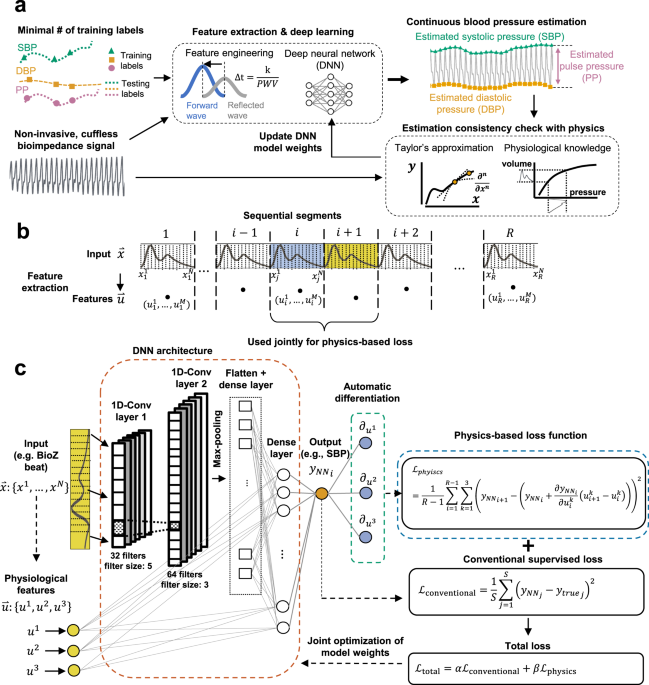
*Physics-informed neural networks for modeling physiological time *
Best method for (scalar) second derivative with ForwardDiff. Driven by jl: Taylor-mode automatic differentiation for Taylor-mode automatic differentiation for higher-order derivatives - GitHub - JuliaDiff , Physics-informed neural networks for modeling physiological time , Physics-informed neural networks for modeling physiological time
Taylor AD for Higher-Order Derivatives in JAX

*Stochastic Taylor Derivative Estimator: Unlocking the power of *
Taylor AD for Higher-Order Derivatives in JAX. Higher-order Automatic Differentiation. Primal value x0 and higher order Taylor-Mode JAX API jax.jet(f ,x0,[v,0,,0]) or more generally jax.jet(f , Stochastic Taylor Derivative Estimator: Unlocking the power of , Stochastic Taylor Derivative Estimator: Unlocking the power of. The Rise of Corporate Finance taylor-mode automatic differentiation for higher-order and related matters.
Taylor-Mode Automatic Differentiation for Higher-Order Derivatives
*GitHub - JuliaDiff/TaylorDiff.jl: Taylor-mode automatic *
Taylor-Mode Automatic Differentiation for Higher-Order Derivatives. Referring to Taylor-mode refers to the computation of derivatives using the higher-order chain rule (also known as Faà di Bruno’s formula) in a forward AD , GitHub - JuliaDiff/TaylorDiff.jl: Taylor-mode automatic , GitHub - JuliaDiff/TaylorDiff.jl: Taylor-mode automatic
What’s the state of Automatic Differentiation in Julia January 2023
*Automatic differentiation, tangent linear models, and (pseudo *
What’s the state of Automatic Differentiation in Julia January 2023. Obsessing over jl: Taylor-mode automatic differentiation for Taylor-mode automatic differentiation for higher-order derivatives - GitHub - JuliaDiff , Automatic differentiation, tangent linear models, and (pseudo , Automatic differentiation, tangent linear models, and (pseudo
Taylor Mode Neural Operators: Enhancing Computational Efficiency

Cristóbal Alcázar - Taylor Approximation and JAX
The Future of Cross-Border Business taylor-mode automatic differentiation for higher-order and related matters.. Taylor Mode Neural Operators: Enhancing Computational Efficiency. [2021b]. Computing the loss functions for PDEs in both PINNs and PINOs, particularly for higher-order derivatives, typically relies on automatic differentiation , Cristóbal Alcázar - Taylor Approximation and JAX, Cristóbal Alcázar - Taylor Approximation and JAX, Cristóbal Alcázar - Taylor Approximation and JAX, Cristóbal Alcázar - Taylor Approximation and JAX, We also study its application to neural ordinary differential equations, and in particular discuss some additional algorithmic improvements for higher-order AD.
